P9111 [福建省队集训2019] 最大权独立集问题

题意

给定一颗 nn 点的树，点有权值 did_i。

有操作：

  • 选择一个点 uu，对于该点所有连边且之前未被选择过的点 vv，使得 dv←dv+dud_v\leftarrow d_v+d_u，然后该点删除，对答案贡献 dud_u。

确定选择顺序，求 max⁡∑i=1ndu\max \sum_{i=1}^n d_u。

注意：对于每次操作 did_i 都继承新的权值 di+xd_i+x。其实就是不区分 did_i 和 di′d_i'，即 did_i 每次都是最新的值。

数据范围：保证 ∣di∣≤109\left|d_i\right| \le 10^9，1≤ci<i1 \le c_i \lt i，1≤n≤4001\le n \le 400。

思路

首先若一个点被选择后，那么他的贡献会具有传递性，传递给之后所有还未被选择的点。

那么设 tut_u 为点 uu 被选择的时间，若 tu<tvt_u<t_v 我们连 u→vu\rightarrow v 即代表着权值 dud_u 流向 dvd_v，注意这里的 dud_u 可能也继承着别的点流向 uu 的 did_i。

此题因此转化为给每条边定向求得最大权值。

那我们考虑拆贡献，分别考虑每个 did_i 对答案的贡献的数量，那么答案即为 ans=∑i=1ndi×cntians=\sum_{i=1}^n d_i\times cnt_i，dd 为点权，cntcnt 为点权的贡献次数。

那我们考虑树形 dp 求得答案。

设 fu,i,jf_{u,i,j} 代表已经考虑完点 uu 子树内的贡献，能到的点有 ii 个，其中在其子树（包含自己）内的点有 jj 个。

请理解这里的能到并非单指连向的边，而是能通过有向边传递到的点的个数。这也正是区别于其他树形 dp 特殊的地方。

初始 fu,i,1=duf_{u,i,1}=d_u，请注意这里的 i−1i-1 个额外贡献还未算入其内，我们在转移的时候更新。

那么我们考虑 uu 与 vv 的边的方向。

若 u→vu\rightarrow v，那么 fu,i,j+k⟵maxfu,i,j+fv,k,k+k×duf_{u,i,j+k}\stackrel{max}{\longleftarrow} f_{u,i,j}+f_{v,k,k}+k\times d_u。

对于该种情况我们发现点 vv 的贡献只能流向它的子树中，不会有额外的贡献，因此我们分析得知我们每次定向都会影响点 vv 的流量，因此我们要枚举点 vv 的指出数量 kk，将贡献加入其中，即 fv,k,k+k×duf_{v,k,k}+k\times d_u。

这个图 vv 点不一定都是指出啊，也有可能是 vv 的儿子指入。

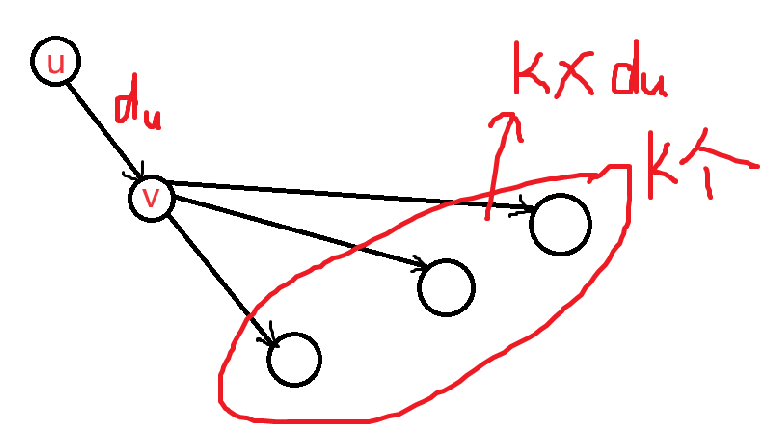
若 u←vu\leftarrow v，那么 fu,i,j⟵maxfu,i,j+fv,i+k,kf_{u,i,j} \stackrel{max}{\longleftarrow}f_{u,i,j}+f_{v,i+k,k}。

这种情况同理，图就不画了。这种情况下，vv 的贡献也会同时向外流出 i×dvi\times d_v，因此是 fv,i+k,kf_{v,i+k,k}。

fu,i,j=fu,i,j+(i−j)×duf_{u,i,j}=f_{u,i,j}+(i-j)\times d_u 这里就是类似于费用提前计算的思想将额外 (i−j)×du(i-j) \times d_u 的贡献加入其内。

强调：

  • 注意转移不能有后效性，必须得从上一个的去更新，因此就是得临时存一下 fu,i,jf_{u,i,j} 放到 tmpi,jtmp_{i,j}。

  • 还有对于 ff 要初始化为极小值，因为 ∣di∣≤109\left|d_i\right| \le 10^9。

时间复杂度为 O(n3)O(n^3) 易分析。

CODE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<iostream>
#include<vector>
#define int long long
using namespace std;
template<typename T>inline void read(T &x){
    x=0;T f=1;char ch=getchar();
    while(ch<48||ch>57){if(ch=='-'){f=-1;}ch=getchar();}
    while(ch>=48&&ch<=57){x=x*10+ch-48;ch=getchar();}
    x*=f;
}
template<typename T>inline void write(T x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+48);
}
const int N=408;
int d[N],c[N];
int n,ans;
vector<int> G[N];
int f[N][N][N];
int sz[N];
int tmp[N][N];
void dfs(int u,int fa){
    sz[u]=1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            f[u][i][j]=-1e18;
        }
    }
    for(int i=1;i<=n;i++){
        f[u][i][1]=d[u];
    }
    for(auto v:G[u]){
        if(v==fa) continue;
        dfs(v,u);
        for(int i=1;i<=n;i++){
            for(int j=1;j<=sz[u]&&j<=i;j++){
                tmp[i][j]=f[u][i][j];
                f[u][i][j]=-1e18;
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=sz[u]&&j<=i;j++){
                for(int k=1;k<=sz[v]&&j+k<=i;k++){
                    f[u][i][j+k]=max(f[u][i][j+k],tmp[i][j]+f[v][k][k]+k*d[u]);
                }
                for(int k=1;k<=sz[v];k++){
                    f[u][i][j]=max(f[u][i][j],tmp[i][j]+f[v][i+k][k]);
                }
            }
        }
        sz[u]+=sz[v];
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=sz[u]&&j<=i;j++){
            f[u][i][j]+=d[u]*(i-j);
        }
    }

signed main(){
    read(n);
    for(int i=1;i<=n;i++){
        read(d[i]);
    }
    for(int i=2;i<=n;i++){
        read(c[i]);
        G[c[i]].push_back(i);
        G[i].push_back(c[i]);
    }
    dfs(1,0);
    ans=-1e18;
    for(int i=1;i<=n;i++){
        ans=max(ans,f[1][i][i]);
    }
    write(ans);
    return 0;
}

__END__