涂色游戏

涂色会覆盖之前，因此只需要记录每个格子涂色的时间戳，就可唯一确定最终颜色。

幂次

在 $1$ 到 $n$ 中，有多少正整数 $x$ 可以被表示为 $x = a^b$ 的形式，其中 $a, b$ 都是正整数，且 $b \geq k$。

对于所有数据，保证 $1 \leq n \leq 10^{18}$，$1 \leq k \leq 100$。

此题的关键点就是 $n$ 的范围很大，因此我们考虑容斥。

对于 $k=1$，有 $\sqrt[1]{n}$ 个，已经包含所有数，无需在讨论后续。

对于 $k=2$，有 $\sqrt[2]{n}$ 个,约有 $1e9$ 个，但是我们知道 对于 $1-n$ 中共有 $\lfloor\sqrt[2]{n}\rfloor$ 个平方数，这类似于 $1-n$ 中共有 $\lfloor \frac{n}{k} \rfloor$ 个 k 的倍数，因此只要把对于 $k>2$ 的重复统计的容斥掉即可。

对于 $k>3$，有 $\sqrt[3]{n}$ 个，是 $1e6$ 因此暴力枚举即可。

$\color{red}{对于k>3记得记录1的贡献}$。

这是在优化暴力枚举+基础数论知识。

复杂度 $O(\sqrt[3]{n})$，这个非常不严谨，但是我不会算了。

还有更优秀的解法，但是不好想

设 $g_i$ 为 $[1,n]$ 中，$x=a^i$ 的个数，显然 $g_i$ 为 $\sqrt[i]{n}$。

设 $f_i$ 为 $[1,n]$ 中，$x=a^i$ 但是对于 $j>i$，$x_j \neq x_i$。

因此答案为

$$ans= \sum_{i=k}^{60}f_i$$

因为 $2^{60}>1e18$，所以到 $60$ 即可。

因此求得 $f_i$ 只需容斥即可。

$$f_i=g_i-\sum_{idx=2}^{k}f_{i\times idx}$$

含义就是减去所有可以组成他的次幂，因为 $a^i \supseteq a^{2i}$，所以容斥掉即可。

$\color{red}{对于1我们默认先删除，到最后答案 +1 即可}$。

1
2
3
4
5

for(long long i=60;i>=k;i--){
		f[i]=pow<long double>(n,1.0/i)-1;
		for(ll j=i*2*;j<=60;j+=i) f[i]-=f[j];
		ans+=f[i];
	}

复杂度 $O(k \log k)$

圣诞树

逆时针编号依次给定凸包的坐标，让球从凸包最高点 $m$ 最终走完所有顶点的最短距离。

逆时针是对写 $dp$ 方便的。

$\color{red}{最小生成树是假做法}$

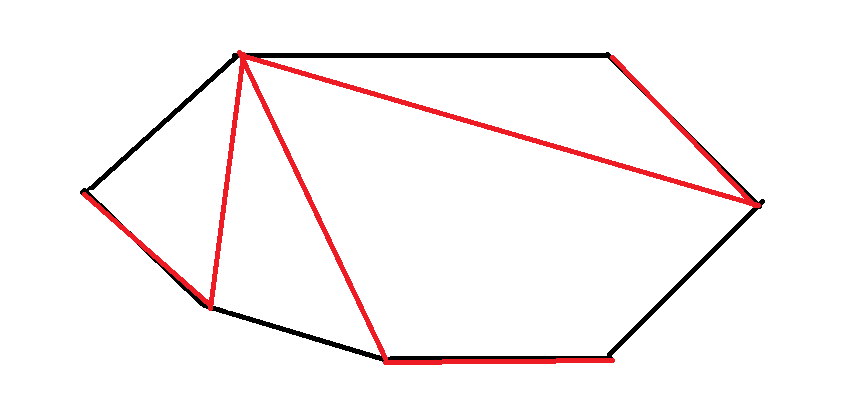
显然这是假的。

考虑正解，对于给定了起点，我们先猜测若路径有交叉，显然不是最优，可以四边形不等式即可证明。

对于至高点两边，在同一侧运动显然是每次直走一个编号的距离，这样一定是最优的，因为隔着走肯定还得返回，路径必然有相交，而且肯定是从最高点每次走离自己比较近的点，依次向下，证明显然。

这题在求出最优的同时还有求解路径，还要保存路径，这个只需在每次转移最优的时候记录一下，最后逆推即可。

因为一直是向前走，$dp$ 无后效性可以记录路径。

因此考虑区间 $dp$。

设 $f_{i,j,0/1}$ 表示为已经走了 $i+j$ 步，至高点左边已经选了 $i$ 个节点，右边已经选择了 $j$ 个节点当前在左边0还是右边1的最短路径。
一下对于不合法编号自动考虑 $+n$ 或 $-n$ 成为合法的。

$$f_{i,j,0}=min(f_{i-1,j,0}+dist(m+i-1,m+i),f_{i-1,j,1}+dist(m+i,m-j))\\ f_{i,j,1}=min(f_{i,j-1,1}+dist(m-j+1,m-j),f_{i,j-1,0}+dist(m+i,m-j))$$

显然是合法且保证正确的。

密码锁

给定一个锁，对于每个拨圈可以上下依次移动。

对于 $1 \leq i \leq k$，定义密码锁第 $i$ 行的松散度为

$$c(i) = \max \limits _ {j = 1} ^ n a _ {i, j} - \min \limits _ {j = 1} ^ n a _ {i, j}$$

同时定义整个密码锁的松散度为

$$C = \max \limits _ {1 \leq i \leq k} c(i)$$

求最小的 $C$ 值。

对于所有数据，保证 $1 \leq T$，$1 \leq k \leq 4$，$1 \leq a _ {i ,j} \leq 3 \times 10 ^ 4$。

考虑随机化，对于该问题我们最难确定的就是对这个矩阵，我们对于其中任意一个元素都难以确定其位置，那我们就考虑先固定住一列，剩下的列在求解，多随机几次一定能获得正解，因为随机一次的复杂度仅有 $nk^2$，随机 $400$ 次这一定是可以获得正解的。

随机就是写个随机，模拟求解一下答案

1

mt19937 g(chrono::_V2::steady_clock::now().time_since_epoch().count());

$\color{green}{正解，先鸽了}$

__END__